Tipe : Les cyclones tropicaux
Menu principal:
III) Une étude thermodynamique
Nous allons étudier un modèle simplifié de théorie MPI (Maximum Potential Intensity) (IMP en français) : il calcule l'intensité que pourrait avoir un cyclone s'il exploitait au maximum les ressources énergétiques de son environnement. En réalité, d'autres facteurs empêchent le cyclone d'atteindre les valeurs que nous pourrions prévoir, comme la dynamique interne du cyclone, l'environnement atmosphérique ou océanique (à cause des circulations d'eau provoquées par la circulation du vent). Il est donc normal de trouver, pour les cyclones réels, des valeurs plus petites pour la vitesse et plus élevées pour la pression que celles prévues par le modèle. Pour les modèles d'IMP existant, on estime en général qu'environ 2/3 des cyclones atteignent 50% de l'IMP, et seuls 1/5 environ dépassent 75% de l'IMP.
1°) Définitions des variables
a) Variables classiques et unités
- P pression en pascal (Pa)
- T température en kelvin (K)
- r : densité (kg.m^-3)
- L chaleur latente de vaporisation
- C capacité calorifique à pression constante
- R la constante des gaz parfaits R=8.314 J·K^-1·mol^-1
b) Variables thermodynamiques
- Pression réduite 
- Température potentielle ![]() Elle est conservée lors de mouvements adiabatiques secs (sans changement d’état de l’eau).
Elle est conservée lors de mouvements adiabatiques secs (sans changement d’état de l’eau).
- rapport de mélange ![]()
- Température potentielle équivalente : ![]() Elle est conservée lors de mouvements «pseudo-adiabatiques» (sans gain ni perte de chaleur autres que ceux associés aux changements de phase de l’eau) secs et humides.
Elle est conservée lors de mouvements «pseudo-adiabatiques» (sans gain ni perte de chaleur autres que ceux associés aux changements de phase de l’eau) secs et humides.
- Entropie «humide» : ![]()
- Variation de chaleur totale : ![]()
c) Variables dynamiques
- Equilibre hydrostatique![]()
- Equilibre du vent gradient(la variation radiale de pression équilibre la force centrifuge)
![]()
O le centre du cyclone, P le point considéré, r=OP
v est la vitesse tangentielle (on suppose que la vitesse et l’accélération radiale est bien inférieure a la vitesse tangentielle)
f est le terme de Coriolis dû à la rotation de la Terre (vertical). ![]() ; T période de rotation de la terre (soit environ T=24.3600 s= 86s)LAT = la latitude en degrés.
; T période de rotation de la terre (soit environ T=24.3600 s= 86s)LAT = la latitude en degrés.
- Moment angulaire absolu ![]() Quantité conservative lors des mouvements radiaux en l’absence de frottements ou de force mécanique appliquée.
Quantité conservative lors des mouvements radiaux en l’absence de frottements ou de force mécanique appliquée.
2°) Circulation radiale dans un cyclone

De A à B Par suite du frottement à la surface de l’océan, l’air se charge en humidité (presque jusqu’à saturation). La chaleur totale augmente et le moment angulaire diminue, d’où une perte d’énergie cinétique pour le système.
De B à C Au cours du mouvement ascendant, la chaleur latente (iela vapeur d’eau gagnée lors de la phase AB) se transforme en chaleur sensible par condensation. La chaleur totale ainsi que le moment angulaire absolu restent constants.
De C à D A grande distance de l’œil du cyclone, l’excès de chaleur latente disparaît par rayonnement infrarouge vers l’espace et le moment angulaire augmente à nouveau par interaction avec la circulation atmosphérique de grande échelle.
De D à A L’air redescend dans un lent mouvement de subsidence en conservant sa chaleur totale et son moment angulaire.
Le point A est situé au niveau des premières isobares fermées et la vitesse tangentielle y est nulleV=0. B est au niveau de vent tangentiel maximum V.
3°) Cycle de Carnot équivalent
a) Variables dynamiques
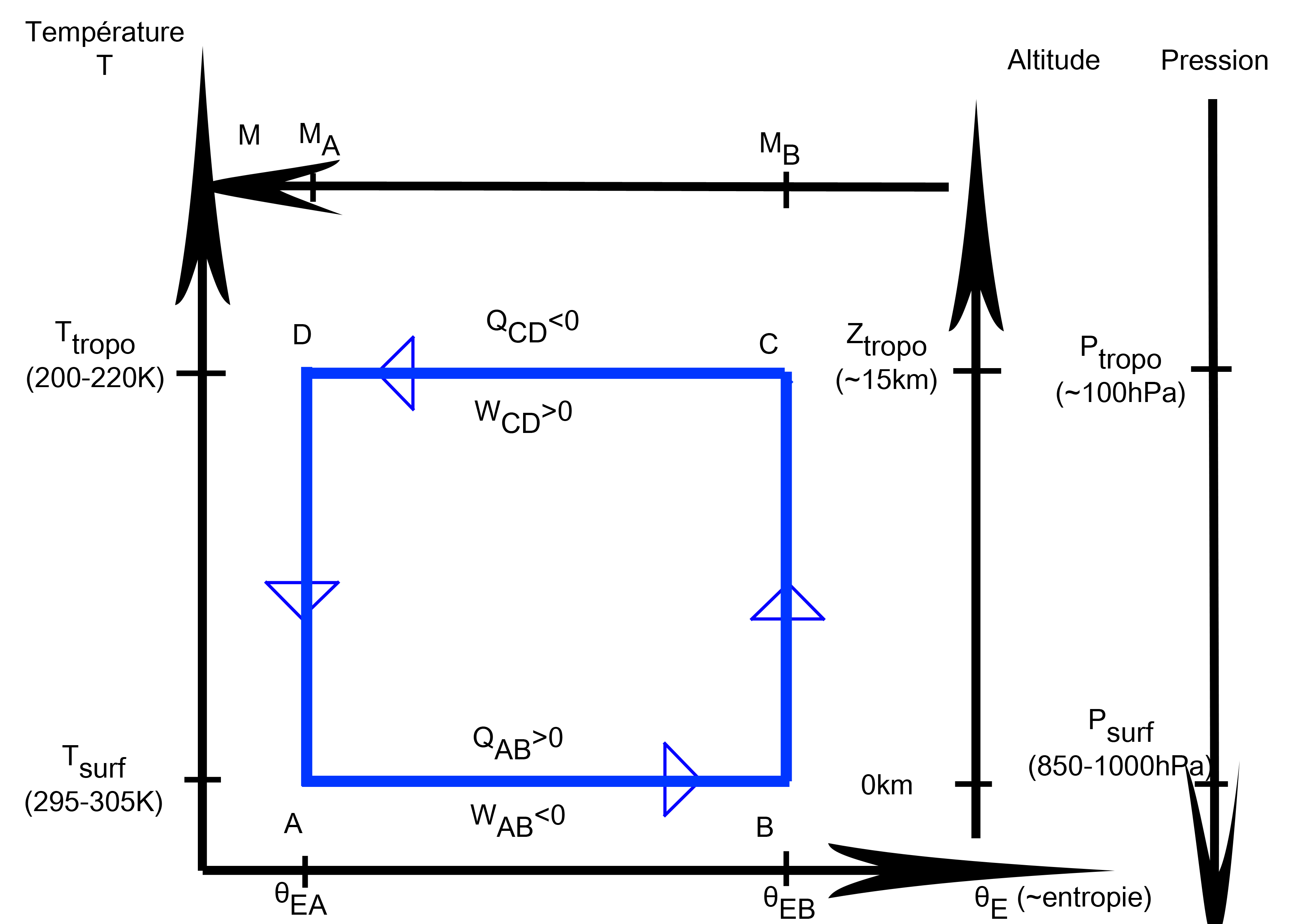
AB L'air gagne de la chaleur totale (Q>0) et perd de l'énergie cinétique (W<0), la transformation est isotherme.
BCLa transformation de chaleur latente en chaleur sensible est adiabatique réversible (ieisentropique) et s'effectue à moment angulaire constant.
CDL'air perd de la chaleur totale (Q<0) et gagne de l'énergie cinétique (W>0), la transformation est isotherme.
DALe réchauffement par compression adiabatique, sans transformation entre chaleurs latente et sensible, est isentrope et s'effectue à moment angulaire constant.
On a :
![]()
b) Chaleur totale
Comme dans la branche AB: ![]() et dans ma branche CD
et dans ma branche CD ![]() .
.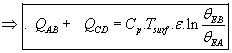
Avec ![]() : efficacité thermodynamique
: efficacité thermodynamique![]()
c) Energie cinétique
Sur la branche CD ![]() et
et ![]()
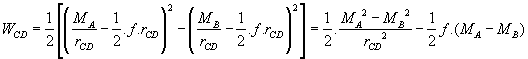
![]() si
si ![]() >>
>>
Or ![]() est déterminé par le rayon
est déterminé par le rayon ![]() où la vitesse tangentielle est nulle et
où la vitesse tangentielle est nulle et ![]() est déterminé par .
est déterminé par .
le rayon ![]() où la vitesse tangentielle
où la vitesse tangentielle ![]() est maximum.
est maximum.![]()
Sur la branche AB
Equation de Bernoulli ![]()
Donc 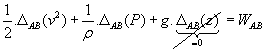
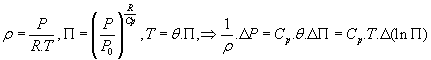
![]()

d) Cycle de Carnot![]()
![]()
On utilise l'équation du vent gradient :
On obtient finalement :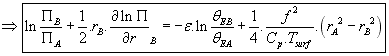
Pour obtenir une estimation de la pression au centre du cyclone ![]() on suppose que
on suppose que ![]() et que
et que ![]() <<
<<
On suppose également que ![]() car
car ![]()
Et ainsi :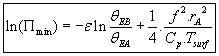
![]() :
:![]()
![]()
![]() car
car ![]()
Expression du rapport de mélange: ![]() avec
avec ![]() le rapport de mélange à saturation
le rapport de mélange à saturation
H=humidité relative (comprise entre 0 et 1)
On prend ![]()
![]() et donc finalement :
et donc finalement :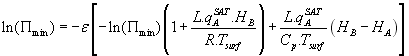
ce qui nous donne 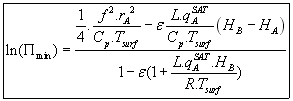
4°) Application numérique :

Vitesse du vent maximum ![]() :
:
On peut approximer le vent maximum en considérant l'équation du vent gradient:![]()
On suppose que le gradient de pression radial est concentré entre O et ![]()
![]()
dont la solution positive (vent cyclonique) est:![]()
comme ![]()
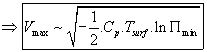
Application numérique pour ![]() =933.4 hPa
=933.4 hPa ![]()
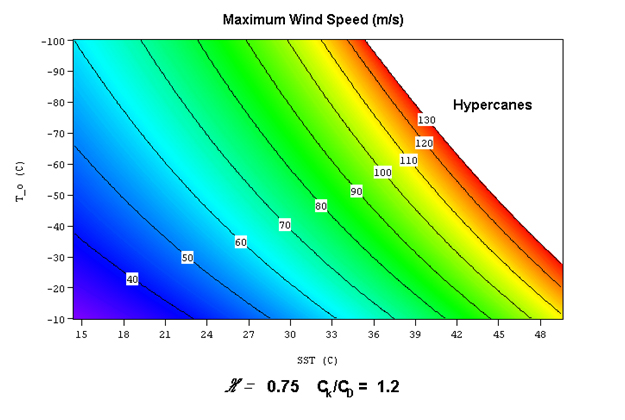

D'après un 'exercice' fait par Frank Roux (Laboratoire d'Aérologie de Toulouse) à partir de :
* Emanuel, K, 1986 An Air Sea interaction théory for tropical cyclones. Part I steady state maintenance ;
* Emanuel, K 1988 The maximum intensity of hurricanes ;
* Emanuel, K, 1987 The dependance of hurricanes intensity on climate ;
* Emanuel, K, 1988 Toward a general theory of hurricanes.